PREGUNTAS FRECUENTES
¿QUE SON LAS FRACCIONES?
Fracciones
Una fracción es una parte de un total
Corta una pizza en trozos, y tendrás fracciones:
 |
 |
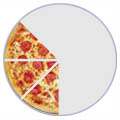 |
| 1/2 | 1/4 | 3/8 |
|
(Una mitad)
|
(Un cuarto)
|
(Tres octavos)
|
| El número de arriba te dice cuántas porciones tienes y el de abajo te dice en cuántos trozos se ha cortado la pizza. | ||
Numerador / Denominador
Al número de arriba lo llamamos Numerador, es el número de partes que tienes.
Al de abajo lo llamamos Denominador, es el número de partes en que se ha dividido el total.
| Numerador |
| Denominador |
¡Sólo tienes que recordar esos nombres! (Si los confundes, recuerda que denominador es con "D" de dividir)
Fracciones equivalentes
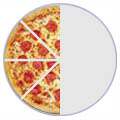
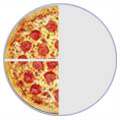
Algnas fracciones parecen diferentes pero en realidad son la misma, por ejemplo:
| 4/8 | = | 2/4 | = | 1/2 | ||
| (Cuatro octavos) | (Dos cuartos) | (Una mitad) | ||||
 |
 |
 |
Normalmente lo mejor es dar la respuesta usando la fracción más simple (1/2 en este caso). Eso se llamaSimplificar o Reducir la fracción.
Sumar fracciones
Puedes sumar fracciones fácilmente si el número de abajo (el denominador) es el mismo:
| 1/4 | + | 1/4 | = | 2/4 | = | 1/2 | ||
| (Un cuarto) | (Un cuarto) | (Dos cuartos) | (Una mitad) | |||||
 |
 |
 |
 |
Otro ejemplo:
| 5/8 | + | 1/8 | = | 6/8 | = | 3/4 | ||
 |
 |
 |
 |
Sumar fracciones con denominadores diferentes
¿Y si los denominadores no son iguales? Como en este ejemplo:
| 3/8 | + | 1/4 | = | ? | ||||
 |
 |
 |
 |
Deberías hacer que los denominadores fueran iguales de alguna manera. En este caso es fácil, porque sabemos que 1/4 es lo mismo que 2/8 :
| 3/8 | + | 2/8 | = | 5/8 | ||||
 |
 |
 |
 |
En ese ejemplo fue fácil hacer que los denominadores fueran el mismo, pero puede ser más difícil... visita las páginas de los métodos de
¿COMO SIMPLIFICAR FRACCIONES?
Simplificando Fracciones
Para simplificar una fracción, divide los números de arriba y abajo por el mayor número que
divida a los dos exactamente.
Simplificando Fracciones
Simplificar (o reducir) fracciones significa hacer la fracción lo más simple posible. ¿Por qué decir cuatro octavos (4/8) cuando en realidad quieres decir la mitad (1/2) ?
| 4/8 | ==> | 2/4 | ==> | 1/2 | ||
| (Cuatro octavos) | (Dos cuartos) | (Un medio) | ||||
 |
 |
 |
¿Cómo simplifico una fracción?
Hay dos maneras de simplificar una fracción:
Método 1
Intenta dividir los números de arriba y abajo de la fracción a la vez hasta que no puedas seguir más (prueba a dividirlos por 2,3,5,7,... etc).
Ejemplo: Simplifica la fracción 24/108 :
| ÷ 2 | ÷ 2 | ÷ 3 | ||||
| 24 | = | 12 | = | 6 | = | 2 |
| 108 | 54 | 27 | 9 | |||
| ÷ 2 | ÷ 2 | ÷ 3 | ||||
Método 2
Divide las dos partes de la fracción por el Máximo Factor Común (¡tienes que calcularlo primero!).
Ejemplo: Simplifica la fracción 8/12 :
1. El mayor número que divide exactamente 8 y 12 es 4 (¿por qué?), así que el Máximo Factor Común es 4.
2. Divide arriba y abajo por 4:
| ÷ 4 | ||
| 8 | = | 2 |
| 12 | 3 | |
| ÷ 4 | ||
Simplificando Fracciones Automáticamente
Bueno, hay un tercer método, usa esta herramienta:
¿QUE SON FRACCIONES EQUIVALENTES?
Fracciones Equivalentes
Las Fracciones Equivalentes tienen el mismo valor, aunque parezcan diferentes.
Estas fracciones son en realidad lo mismo:
| 1 | = | 2 | = | 4 |
| 2 | 4 | 8 |
¿Por qué son lo mismo? Porque cuando multiplicas o divide a la vez arriba y abajo por el mismo número, la fracción mantiene su valor. La regla a recordar es:
¡Lo que haces a la parte de arriba de la fracción
también lo tienes que hacer a la parte de abajo!
Por eso, estas fracciones son en realidad la misma:
| × 2 | × 2 | |||
|
|
||||
| 1 | = | 2 | = | 4 |
| 2 | 4 | 8 | ||
|
|
||||
| × 2 | × 2 | |||
| 1/2 | 2/4 | 4/8 | ||
 |
= |  |
= |  |
Aquí hay más fracciones equivalentes, esta vez dividiendo:
| ÷ 3 | ÷ 6 | |||
| 18 | = | 6 | = | 1 |
| 36 | 12 | 2 | ||
| ÷ 3 | ÷ 6 | |||
Si seguimos dividiendo hasta que no podamos más, habremos simplificado la fracción (la hemos hecho la más simple posible).
Importante:
- Las partes de arriba y abajo de la fracción siempre deben ser números enteros.
- Las operaciones que podemos hacer son multiplicar y dividir (siempre las dos partes a la vez). Si sumamos o restamos un número arriba y abajo, no tendremos una fracción equivalente.
- El número que elijas para dividir las dos partes no debe dejar ningún resto en las divisiones.
¿COMO SUMAR FRACCIONES?
Sumar fracciones
Hay tres simples pasos para sumar fracciones:
Paso 1: asegúrate de que los números de abajo (los denominadores) son iguales
Paso 2: suma los números de arriba (los numeradores). Pon la respuesta sobre el denominador del paso 1
Paso 3: simplifica la fracción (si hace falta)
Ejemplo 1:
| 1 | + | 1 |
| 4 | 4 |
Paso 1. Los números de abajo son los mismos. Ve directamente al paso 2.
Paso 2. Suma los números de arriba y pon la respuesta sobre el denominador:
| 1 | + | 1 | = | 1 + 1 | = | 2 |
| 4 | 4 | 4 | 4 |
Paso 3. Simplifica la fracción:
| 2 | = | 1 |
| 4 | 2 |
(Si no estás seguro de cómo se hace el último paso ve a la página de Fracciones equivalentes)
Ejemplo 2:
| 1 | + | 1 |
| 3 | 6 |
Paso 1: los números de abajo son diferentes. Así que necesitamos hacerlos iguales.
Podemos multiplicar arriba y abajo de 1/3 por 2 así:
| 1 | = | 2 |
| 3 | 6 |
y ahora los números de abajo (los denominadores) son iguales, nuestro problema queda así:
| 2 | + | 1 |
| 6 | 6 |
Paso 2: suma los números de arriba y ponlos sobre el mismo denominador:
| 2 | + | 1 | = | 2 + 1 | = | 3 |
| 6 | 6 | 6 | 6 |
Paso 3: simplifica la fracción:
| 3 | = | 1 |
| 6 | 2 |
